四 角錐 体積 公式 716602

錐體體積公式錐體的體積 Kalpff

求め方 1 、 1 辺の長さから正方形の面積を求める ・ 1 辺の長さは 5 ・ 正方形の面積 = 5 × 5 = 25 正四角錐の体積の求め方 1 − 2 2 番目に、正方形の面積に高さと 1 3 を掛けます。 求め方 2 、正方形の面積に高さと 1 3 を掛ける ・ 正方形の面積は 25 、高 同じ答に 公式でもあるのかと考えると 四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業が

四 角錐 体積 公式

四 角錐 体積 公式-四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。角錐や円錐の体積の公式はこれと似ています。同じように、底面積と高さを掛けます。その後、 3分の1にすることで体積が出ます。 つまり、角錐と円錐の体積を出す公式は以下のようになります。 角錐・円錐の体積 = 底面積 × 高さ × $\displaystyle\frac{1}{3}$

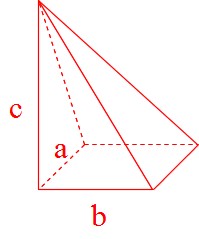
Mathematics 角錐の体積が角柱の３分の１になる証明 働きアリ

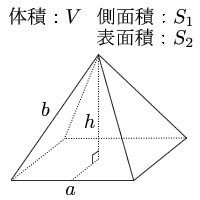
 雑学34「錐」の体積はなぜ「柱」の3分の1なのか これら立体の体積Vの公式は、底面積Sと高さhを使って、 名称としては、もちろん四角錐。 角錐と円錐の体積 角錐と円錐の体積も同じ公式です。 底面積を S S 、高さを h h とすると、体積 V V は以下の公式になります。 V = 1 3 Sh V = 1 3 S h 公式に 1 3 1 3 が付いている理由は、高校数学で積分を習うとわかります。 難しい計算なので、今は無理矢理 1 立方体の体積は、（その面が6つありますので）この四角錐6つに分解できます。 そのため、この四角錐の体積は 四角錐の体積＝底面積×高さ／3 です。 リンク： 三角錐の重心（四面体の重心） 正四面体の高さと表面積と体積V 正四面体に外接する球の半径R

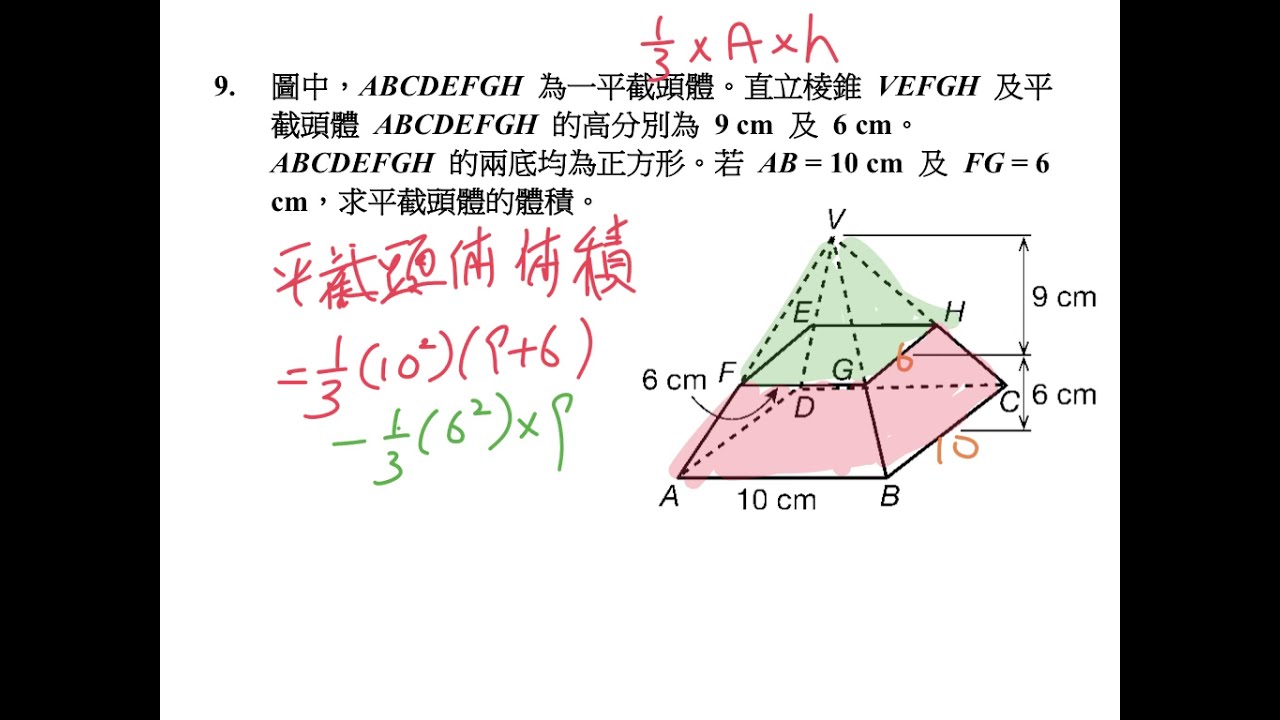
 四角錐台の体積の公式について。 この画像のように上下面が共に長方形、BC//FG 及び CD//GHとする四角錐台の体積が h/6(XyxY2(XYxy)) となる事を証明したいです。 この公式になるまでの説明と経緯を教えて下さい。 宜しくお願いします。 ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積を拡縮してみる ①特別な四角錐を考える 底面積が一辺 の正方形，高さが の四角錐を考える． これを6つ組み合わせる． この立方体の体積＝ 1つの四角錐の体積は次式で表される． こんにちは。相城です。今回は球の体積の何で？にお答えできればと存じます。 球の体積の公式のなぜ？ 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。

四 角錐 体積 公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	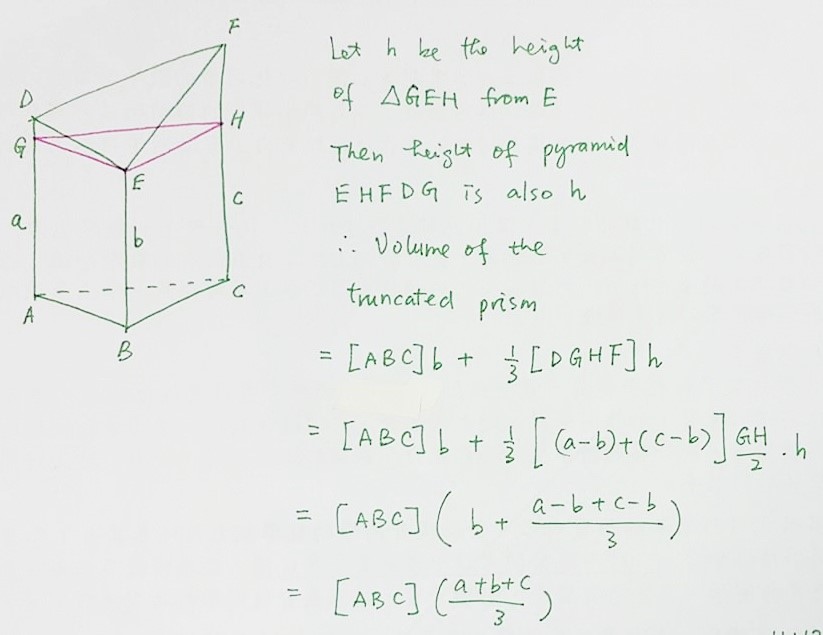平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦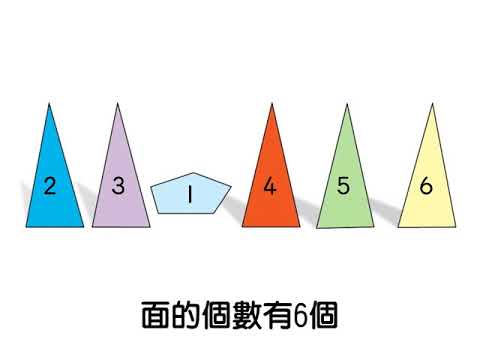
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦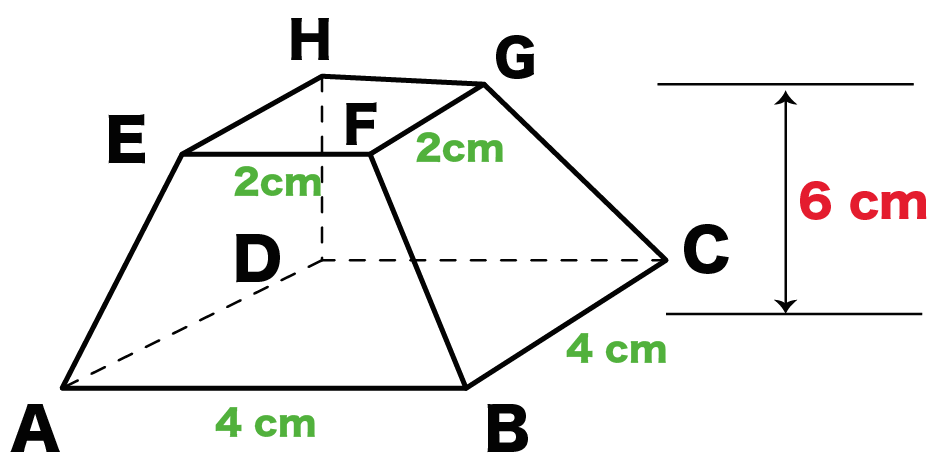
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦
平行六面體的體積 老王的夢田 痞客邦	平行六面體的體積 老王的夢田 痞客邦

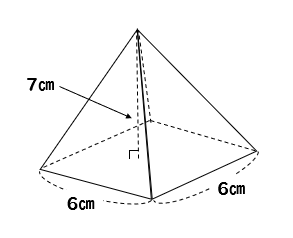
錐台（すいだい、英 Frustum ）は、錐体から、頂点を共有し相似に縮小した錐体を取り除いた立体図形であり、切頭錐体ともいう。 あるいは言い換えれば、錐体面と2枚の平行な平面によって囲まれる立体図形である。 円錐からできる錐台を円錐台（切頭円錐）、角錐からできる錐台を角錐台四角錐の体積＝(35)÷2×4×6÷3＝32cm 3 です。 角錐の体積の公式は？1分でわかる公式、柱体の体積との違い、3分の1になる証明